
L’analyse d’erreur surprenante étudiée ici concerne le domaine des mathématiques en école primaire, plus précisément en fin de cycle 2. Nous établirons d’abord le contexte pratique, pédagogique et didactique de la situation d’apprentissage qui a révélé l’erreur surprenante, ensuite nous analyserons cette erreur a priori et a posteriori, enfin nous décrirons les remédiations mises en œuvre et possibles par la suite.
L’erreur surprenante a été révélée au cours d’une première séance d’Activités Pédagogiques Complémentaires, avec cinq élèves de CE2 (cycle II) provenant de trois classes différentes, en début de période 2 (novembre/décembre). La séquence proposée pour ces APC concernait la compétence «Poser et calculer des additions avec des nombres jusqu’à 1000» ; il s’agissait d’idendtifier les difficultés de chacun des élèves et de leur apporter un étayage personnalisé pour l’entraînement d’un savoir en cours de construction avec leur enseignant respectif. La première séance d’APC avait donc fonction d’évaluation diagnostique. La compétence travaillée du Programme d’enseignement du cycle des apprentissages fondamentaux (cycle 2) en jeu était Calculer avec des nombres entiers : mettre en œuvre un algorithme de calcul posé pour l’addition, en lien avec le domaine du socle Les systèmes naturels et les systèmes techniques qui précise que«la pratique du calcul, l’acquisition du sens des opérations (…) permettent l’observation, suscitent des questionnements et la recherche de réponses, donnent du sens aux notions abordées».
La progression de la séance d’additions posées allait du plus simple au plus compliqué, jusqu’à l’apparition de l’erreur. Les additions sont données à l’oral par le Professeur des Écoles (P.E). Les élèves travaillent avec un cahier d’essai, un crayon de bois, une gomme et une règle et ont à leur disposition du matériel de manipulation (blocs de base 10). Ils travaillent d’abord de manière individuelle, puis confrontent et expliquent leur résultat et leur procédure avant une mise en commun dirigée par le P.E.
Il est demandé que l’addition soit posée, même pour les cas les plus simples, pour insister sur l’alignement en colonne des nombres.
— addition de deux nombres à un chiffre, sans retenue (ex.3+4)
— addition de deux nombres à un chiffre, avec retenue (ex.7+5)
— addition d’un nombre à un chiffre et d’un nombre à deux chiffres, sans retenue (ex.12+5)
— addition d’un nombre à un chiffre et d’un nombre à deux chiffres, avec retenue (ex.19+4)
— addition de deux nombres à deux chiffres, sans retenue (ex.11+33)
— addition de deux nombres à deux chiffres, avec retenue (ex.24+18)
— addition d’un nombre à trois chiffres et d’un nombre à deux chiffres, sans retenue (ex.123+35)
À ce moment arrive l’erreur surprenante d’un élève dont voici la restitution :
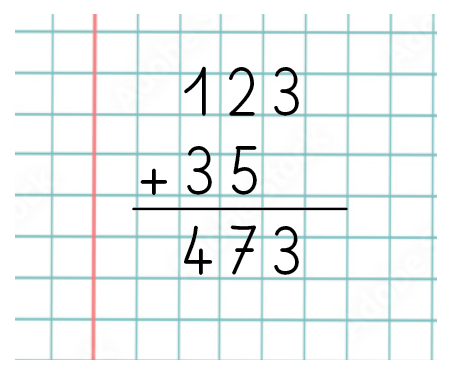
L’objectif de la séance et les critères de réussite ont été énoncés («vous aurez réussi si vos additions en colonne sont posées correctement, c’est à dire si les chiffres sont bien alignés, si vos calculs sont justes et que vous pensez à la retenue»). L’énoncé de la nécessité de «bien aligner les chiffres en colonne» peut induire l’élève en erreur, il peut penser qu’il faut les aligner «pour faire un effort de présentation et faire joli», et non pas parce que la position du chiffre définit sa valeur. On sait pourtant que la procédure de l’addition posée a déjà été étudiée en classe avec l’enseignant. Les principales difficultés de l’addition posée résident dans alignement des unités avec les unités, des dizaines avec des dizaines, des centaines avec les centaines, etc., ne mettre qu’un seul chiffre par colonne, gérer la retenue, comprendre la notion de valeur de position.
L’espace vide engendre un problème. L’élève choisit d’aligner à gauche, comme on le ferait pour l’écriture. La notion de numération positionnelle n’est pas intégrée. Comme on écrit les nombres en base 10, chaque valeur associée aux positions est, en fait, une puissance de 10. L’élève ne se rend pas compte qu’il additione 350 à 123.
Le premier retour pour l’élève est celui de ses camarades ; c’est alors l’occasion qu’ils expliquent pourquoi l’élève s’est trompé, qu’ils verbalisent avec leurs propres mots la procédure à mettre en place. Ils doivent justifier en expliquant quelle valeur a quel chiffre en fonction de sa position. On en vient à la constatation que l’opération est mal posée : certes les chiffres sont alignés, mais des unités ont été glissées dans la colonne des dizaines et des dizaines dans la colonne des centaines. Pour rendre visible et palpable cet état de fait, on utilise les cubes base 10 pour créer 50 unités (et non 5) et 3 centaines (et non 3 dizaines). Ce qu’a produit ce décalage des chiffres est alors pleinement visible.
Le P.E. rappelle ensuite que méthode et rigueur sont indispensables, qu’on ne doit avoir qu’un chiffre par colonne. Il rappelle aussi le sens de lecture (de droite à gauche, on commence par les unités, puis les dizaines, etc.). L’utilisation des tableaux de positionnement des chiffres permet de vérifier les résultats.
Par la suite, on pourra par exemple organiser un «Jeu du banquier» à deux avec abaques, pour renforcer la compréhension de la règle d’échange 1 pour 10, pour amener les élèves à prendre conscience que la position d’un élément sur un support peut suffire à servir de convention pour en déterminer la valeur : quand on a dix jetons sur une tige, on les échange contre un jeton placé sur la tige située à gauche. Chaque position successive vers la gauche indique une valeur dix fois plus importante que celle juste à droite.
Cette «erreur surprenante» a révélé que la notion de valeur de position n’était pas assimilée par l’élève. Les procédures mécaniques qu’il utilisait, sans mettre de sens, ont montré leurs limites quand il a fallu aller un peu plus loin dans la complexité de l’addition posée. La confrontation avec les pairs, la manipulation ont pu raviver l’importance de cette notion d’échange 1 pour 10 et que l’élève y mette du sens.